Diese Seite funktioniert nur mit Javascript.
Durchschnitts- und Grenzkosten3.4.2 Betriebsminimum, -optimumAngebotsfunktion
as Betriebsoptimum und das Betriebsminimum kann man als Mengen, Preise oder auch Preis-Mengen-Kombinationen begreifen. Der Schnittpunkt von Grenzkosten und variablen durchschnittlichen Kosten ist das Betriebsminimum, der Schnittpunkt mit den totalen durchschnittlichen Kosten das Betriebsoptimum. Da die Grenzkostenkurve die beiden anderen jeweils in deren Minima schneidet, kann man ebenso formulieren, dass Betriebsminimum und -optimum den Minima der durchschnittlichen variablen bzw. durchschnittlichen totalen Kosten entsprechen. Auf lange Sicht fallen beide zusammen, da langfristig alle Kosten variabel sind.
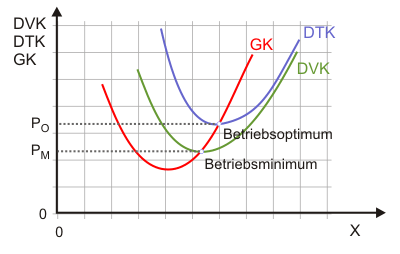
Wenn der Produktpreis $p_x$ unter das Betriebsminimum $p_M$ fällt, wird das Unternehmen seine Produktion kurzfristig einstellen. Es macht dann einen geringeren Verlust als wenn es produzieren würde. Werden nämlich nicht die variablen Kosten gedeckt, dann steigt mit jeder produzierten Einheit der Verlust. In der Betriebswirten eigenen Sprache würde man sagen, der Stückdeckungsbeitrag ist negativ. Wird nichts produziert, entsteht kurzfristig ein Verlust in Höhe der fixen Kosten. Liegt der Preis zwischen $p_M$ und $p_O$, wird zwar mit Verlust produziert, der allerdings geringer ist als die fixen Kosten, da ein positiver Deckungsbeitrag erzielt wird.
Wenn der Preis dem Betriebsoptimum entspricht $p_O$ oder höher liegt, kann die Unternehmung langfristig am Markt bestehen. Der Begriff führt etwas in die Irre, denn ein Preis in Höhe von $p_O$ ist für die Unternehmung nicht optimal. Aus ihrer Perspektive kann der Preis gar nicht hoch genug sein. Optimal ist der Preis in dem Sinn, dass den Konsumenten auf Dauer das Produkt privatwirtschaftlich nicht zu einem günstigeren Preis angeboten werden würde. Sie sind es also, die hier am besten abschneiden. Das ist schließlich auch das Ziel des Wirtschaftens: die Präferenzen der Wirtschaftssubjekte in ihrer Eigenschaft als Konsumenten bestmöglich zu befriedigen. Ausführlich wird der Begriff der gesellschaftlichen Optimalität im Rahmen der Theorie des Allgemeinen Gleichgewichts diskutiert. Außerdem signalisiert die Produktion im Betriebsoptimum einen minimalen Ressourcenverbrauch bei der Erstellung des Produkts. Bei konstanten Faktorpreisen bedeuten die geringsten Kosten pro Stück zugleich den geringsten (bewerteten) Verbrauch an Ressourcen. Damit ist der Zustand nicht nur ökonomisch, sondern auch ökologisch optimal.
Bei dem in Abbildung 1 angenommenen ertragsgesetzlichen Kostenverlauf ist das Betriebsoptimum mit einer Produktionsmenge in Höhe von $x_O$ eindeutig bestimmt. Bei jeder anderen Produktionsmenge würden höhere Kosten pro Stück anfallen. Es sind auch Kostenverläufe denkbar, bei denen das Betriebsoptimum nicht eindeutig ist. Dazu muss die Stückkostenkurve lediglich ganz oder teilweise waagerecht verlaufen. (Sehr) Häufig findet man das Betriebsminimum (und langfristig das Betriebsoptimum) auch als "Randlösung" bei einer Produktionsmenge von null. Das ist der Fall, wenn die Grenzkosten von Beginn an steigen (dann können die Durchschnittskosten nicht sinken und haben demzufolge kein Minimum). Ein konkretes Beispiel dafür wäre eine Cobb-Douglas-Produktionsfunktion mit einem Homogenitätsgrad kleiner eins.